This page has created related with Enginator5000, which is a software based game engine. This part will include information about coordinate systems, cross product, planes, camera basis vectors, frustum culling etc. over time.

Coordinate Systems

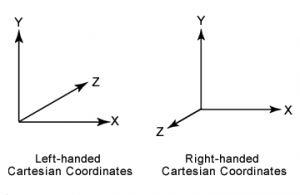
Deciding coordinate system is the first step and the most important thing when you work on computer graphics. 3D graphics applications use two types of Cartesian coordinate systems: left-handed (+z into the screen) and right-handed (+z out to the screen).

Math, physics and OpenGL (except NDC part) use right-hand coordinate system. I also used right-hand coordinate system for Enginator5000.

Cross Product

Cross product is an important operation in computer graphics. With cross product (aka vector product) a new vector orthogonal to the two vectors is calculated (t = r cross s). Cross product is not commutative (I believe sign of the clockwise/counterclockwise angles and sin() operation used in cross product may have an effect on this). This means BxA != AxB. These two operations generate vectors in different directions. For example, if BxA produces a vector C pointing up, AxB produces a vector pointing down (-C).

Direction of the new vector depends on the coordinate system used (left or right handed). The easiest way to find out the direction of the vector:

1. Use your fingers (or index finger) as the 1st vector (for examle B in BxA operation)

2. Use your palm (or middle finger) as the 2nd vector (for examle A in BxA operation)

3. Your thumb will show the direction of the resultant vector

The steps above can be used both for left-handed and right-handed coordinate systems, and if you try, you will see that the direction of the resultant vectors is opposite in different handed coordinate systems.

More details (including dot product) can be found on this page.

Plane

In CG, generally we define a plane using Cartesian form (Ax + By+ Cz + D = 0) with a point and a normal or 3 points (this will also lead us to a point and a normal). Given a point, and a normal (especially if the plane at the origin) is the easiest case. Otherwise:

“Computing the Plane”

Let’s assume we were given P0, P1, P2 points and we want to calculate A, B, C (x, y, and z of the normal) and D (distance to the origin) coefficients.

1. Compute v = P1 – P0 and u = P2 – P0 vectors

2. Compute N = v x u ( N = v.cross(u) ), plane normal and normalize N (Here A = Nx, B = Ny, C = Nz)

3. Compute D = -N . P0 ( D = -N.dot(P0) ). Here, we can take the dot product of any given points (P0, P1, P2). We are using -N because:

As you can see we only need normal of the plane and a point on the plane to define it. 3rd step is optional and only for calculating the distance of the plane to the origin (D).

Distance between a Point and a Plane

Now, we can talk a little about frustum culling. The most basic idea of frustum culling is defining 6 planes (near, far, top, bottom, left, right) and checking the all points whether they are inside the volume set up by these planes. The points outside of the volume will be culled, the points inside the volume (even if they are on the plane) will send for rendering or further culling process.

So, as the most naïve approach, we can take all the points we have in the scene, calculate their distance to the planes, and then decide which of them will be culled.

Let’s assume one of these points is R(Rx, Ry, Rz), and we have our plane Ax + By + Cz + D with normal N. So, the distance between R and the plane is calculated as:

So, distance is simply N.dot(R) + D for any points in the scene, and the sign of the distance tells us whether the point should be culled or not.

* If sign(distance) >= 0 –> the point is in the volume (If the distance is 0, the point is on the plane)

* Else if sign(distance) < 0 –> the point is outside of the volume

Don’t forget, the test above should be done for all 6 planes and even if we get just a case that sign(distance) < 0, this means the point will be culled.

If you think you need more information about the planes, you can check (first 3 links are more math related, last 2 links are CGish) equations of planes in the form Ax + By + Cz = D, finding vector equations of planes,  finding equations of planes using normal vectors or plane tutorial of Songho and Lighthouse3d.

Camera and Camera Basis

We need some information about camera to define frustum, and camera basis vectors to get frustum planes’ normal.

For defining near and far planes (and points on them), we need to know:

* Camera position a.k.a. eye position (camPos)

* Camera look at (The position camera looks) (lookAt)

* Distance to near (dNear) and far planes (dFar)

*  Vertical field of view (fov)

* Ratio between the horizontal and vertical fields of view (ratio)

You can assume distance, fov, and ratio as default constant values; however, especially for real-time applications, you should keep look at and position as class members.

Before calculating basis vectors, remember, we are using right-hand rule. So, we are looking to the screen from +z to -z. Up is +y and our right is +x. So, let’s get started:

For getting basis vectors, we need make some simple calculations. The first vector we will compute is camZ = (camPos – lookAt). This is the vector pointing the opposite direction camera looks. So, this is +z direction (like our world).

For getting the second vector, we will use famous camera up vector (cameraUp). You can give any values that will work for you; however, the most famous (and useful) one is (0, 1, 0). So, now we will get the right vector (camX) of the basis vectors using camX = cameraUp x camZ (camX = cameraUp.cross(camX)) operation.

So, right now, we have a vector pointing +z, one vector pointing +x, and all we need is finding the vector pointing up (+y) using camY = camZ x camX (camY = camZ.cross(camX)).

One important point to keep in my mind, all these camX, camY, camZ vectors should be normalized! And ideally, after you normalized camZ, all the other vectors will have been normalized because of cross product. You can also choose any names for these basis vector. I prefer clear names but, generally people use u, v, w to name them.

Extracting Frustum Planes

// To be continued