Here, you can see a mesh smoothing approach depending on Manifold Harmonics [Vallet et al. 2008] which smooths the mesh by decreasing number of eigenfunctions in use.
You can check this document for the theoretical concept of the approach, and refer Matlab and C++ codes for the implementation. Also, at the end of the page, you can see the results of applying this idea to ambient occlusion:
Matlab Script
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 |
function smoothMeshMHB( filePath, eigenNumber ) % Mesh Smoothing with Manifold Harmonics [Vallet et al. 2008] % INPUTS: % filePath: Path of the mesh you will use % eigenNumber: Number of bases (Eigenvector of the Laplacian) you will use % OUTPUTS: % Displays original and modified version of the mesh %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%% %%% %%% ^-_-^ %%% %%% M. Cihan Ozer - UdeM, LIGUM %%% %%% May 2016, Montreal %%% %%% %%% %%% ALGORITHM: %%% %%% %%% %%% 1. Assemble positive semi-definite discrete Laplacian %%% %%% 2. Compute eigenvectors for the Laplacian for getting MHB %%% %%% 3. Map the bases into canonical basis %%% %%% 4. Transform the mesh into frequency space (MHT) %%% %%% 5. Smooth the mesh %%% %%% 6. Transform the mesh back into geometry space (MHT-1) %%% %%% %%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % NOTES: % - THIS SCRIPT DEPANDS ON GPTOOLBOX (Mesh reading/displaying and computation of % cotangent Laplacian and Hodge star 0): % https://github.com/alecjacobson/gptoolbox % % - If you are using an old version of Matlab, ~ in operations (such as % [vertexNumber, ~] = size(vert)) may give you an error. % In this case you should replace ~ with a variable. % READ MESH FILE [~, remain] = strtok(filePath, '.'); if strcmp('.obj', remain) == 1 [vert, faces] = readOBJ(filePath); %Read OBJ file elseif strcmp('.off', remain) == 1 [vert, faces] = readOFF(filePath); % Read OFF file else disp('Unknown file type!'); end % DISPLAY ORIGINAL MESH figure('name', 'Before MHT'); plot_mesh(vert, faces); % STEP 1: Assemble positive semi-definite discrete Laplacian L = full(cotmatrix(vert, faces)); % Get cotangent Laplacian M = full(massmatrix(vert, faces, 'barycentric')); % Get dual area of vertices (Hodge star 0) Minv = sqrt(inv(M)); % Get M-1/2 for symmetry beltrami = Minv * L * Minv; % Get positive semi-definite discrete Laplacian (Eqauation 2) beltrami = beltrami * -1; % For positive eigenvalues % Handle numerical precision issue: % http://stackoverflow.com/a/33259074 beltrami = (beltrami + beltrami.') * 0.5; % Now our Laplacian is symmetric, and % its eigenvectors are orthonormal % STEP 2: Compute eigenvectors for the Laplacian for getting MHB % Apperantly, eig() function does not give orthogonal eigenvectors % even if the Laplacian is positive semi-definite: % http://www.mathworks.com/matlabcentral/newsreader/view_thread/29459 (First entry) [~, e, eVec] = svd(beltrami); % Sort eigenvectors by increasing eigenvalues (Ascending order) [~, I] = sort(diag(e)); eVec = eVec(:, I); % STEP 3: Map the bases into canonical basis Hktemp = Minv * eVec; Hk = Hktemp(:,1:eigenNumber); % Take only the bases you will use % STEP 4: Transform the mesh into frequency space (MHT) % For this operation, matrix multiplication is much faster than a loop % This operation will give you a row vector Xk = vert(:,1)' * M * Hk; Yk = vert(:,2)' * M * Hk; Zk = vert(:,3)' * M * Hk; % STEP 5-6: Smooth the mesh and transform it back into geometry space (MHT-1) % Allocate memory for vertices [vertexNumber, ~] = size(vert); % Get vertex number dumVertX = zeros(vertexNumber,1); dumVertY = zeros(vertexNumber,1); dumVertZ = zeros(vertexNumber,1); % MHT-1 for k = 1:eigenNumber dumVertX = dumVertX + (Xk(1,k) * Hk(:,k)); dumVertY = dumVertY + (Yk(1,k) * Hk(:,k)); dumVertZ = dumVertZ + (Zk(1,k) * Hk(:,k)); end % MAP NEW VERTEX POSITIONS Vfinal = zeros(vertexNumber,3); Vfinal(:,1) = dumVertX; Vfinal(:,2) = dumVertY; Vfinal(:,3) = dumVertZ; % DISPLAY NEW MESH figure('name', strcat('After MHT: ', int2str(eigenNumber), ' bases is in use')); plot_mesh(Vfinal, faces); end % End of the scrpit |
Output:
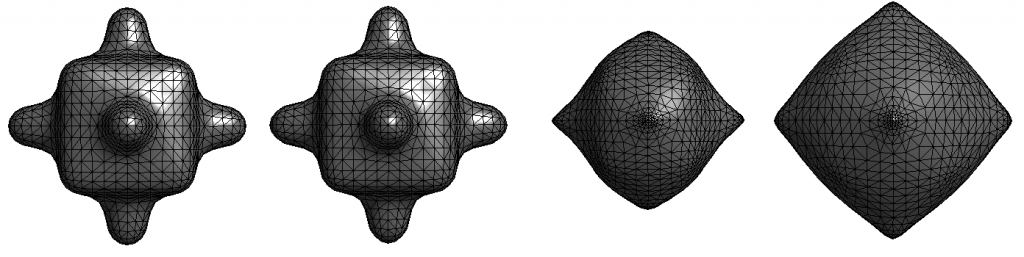
C++ Code Snippet
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
// Mesh Smoothing with Manifold Harmonics [Vallet et al. 2008] // ^-_-^ // M. Cihan Ozer - UdeM, LIGUM // May 2016, Montreal // ALGORITHM: // 1. Assemble positive semi - definite discrete Laplacian // 2. Compute eigenvectors for the Laplacian for getting MHB // 3. Map the bases into canonical basis // 4. Transform the mesh into frequency space(MHT) // 5. Smooth the mesh // 6. Transform the mesh back into geometry space(MHT - 1) // This code depends on Libigl (Mesh reading, displaying and computation of cotangent Laplacian and Hodge star 0) // https://github.com/libigl/libigl // Test scene Eigen::MatrixXd rectangleV(9, 3); Eigen::MatrixXi rectangleF(8, 3); // Bumpy cube Eigen::MatrixXd bumpyV; Eigen::MatrixXi bumpyF; // The current object in display Eigen::MatrixXd currentV, ReV; Eigen::MatrixXi currentF; // For sorting eigenvectors Eigen::VectorXd eigenValues; std::vector sortedIndices; // Helper variables bool isOriginal, isTest; int eigenNumberInUse; int vertexNumber; // MH bases and eigenvectors of Laplacian Eigen::MatrixXd Hk; Eigen::MatrixXd eVec; // Laplacian, Hodge star 0, inverse of Hodge star 0, cotangent laplacian Eigen::SparseMatrix beltrami, M, Minv, L; // Displays evertything, handle user inputs igl::viewer::Viewer viewer; // Init the variables, compute positive semi-definite discrete Laplacian, get MH bases void init() { // Make memory allocations and set variables isOriginal = false; eigenNumberInUse = currentV.rows(); vertexNumber = currentV.rows(); sortedIndices.resize(vertexNumber); ReV.resize(vertexNumber, 3); Hk.resize(vertexNumber, vertexNumber); igl::cotmatrix(currentV, currentF, L); // Compute cotangent Laplace operator: #V by #V igl::massmatrix(currentV, currentF, igl::MASSMATRIX_TYPE_BARYCENTRIC, M); // Compute dual area of the vertices (Hodge star 0) // Get M-1/2 igl::invert_diag(M, Minv); Minv = Minv.cwiseSqrt(); // Set up positive semi-definite discrete Laplacian beltrami = Minv * L * Minv; beltrami = beltrami * -1; // Handle numerical precision issue: http://stackoverflow.com/a/33259074 Eigen::SparseMatrix dummy = beltrami.transpose(); beltrami = (beltrami + dummy) * 0.5; // Apperantly, EigenSolver<> does not give orthogonal eigenvectors even if the Laplacian is positive semi-definite // http://www.mathworks.com/matlabcentral/newsreader/view_thread/29459 (First entry) // But this is slower... Eigen::JacobiSVD es(beltrami, Eigen::ComputeFullV); eigenValues = es.singularValues(); // Get eigenvalues eVec = es.matrixV(); // Get eigenvectors (Left eigenvectors) // Sort eigenvectors by increasing eigenvalues (Ascending order) insertionSort(); // Map the bases into canonical basis // TODO probably slow for (int vi = 0; vi < vertexNumber; vi++) { int next = sortedIndices[vi]; Hk.col(vi) = Minv * eVec.col(next); } } // End of init() // Smooth the mesh with a given eigenfunctions void smooth() { // MHT Eigen::VectorXd Xk = currentV.col(0).transpose() * M * Hk; Eigen::VectorXd Yk = currentV.col(1).transpose() * M * Hk; Eigen::VectorXd Zk = currentV.col(2).transpose() * M * Hk; // Smoothing and MHT-1 Eigen::VectorXd newX = Eigen::VectorXd::Zero(vertexNumber); Eigen::VectorXd newY = Eigen::VectorXd::Zero(vertexNumber); Eigen::VectorXd newZ = Eigen::VectorXd::Zero(vertexNumber); for (int k = 0; k < eigenNumberInUse; k++) { newX = newX + (Xk(k) * Hk.col(k)); newY = newY + (Yk(k) * Hk.col(k)); newZ = newZ + (Zk(k) * Hk.col(k)); } // Map new vertices for (int vi = 0; vi < vertexNumber; vi++) { ReV(vi, 0) = newX(vi); ReV(vi, 1) = newY(vi); ReV(vi, 2) = newZ(vi); } } // End of smooth() int main(int argc, char *argv[]) { // Set the mesh you want to use init(); // Init the variables, compute positive semi-definite discrete Laplacian, get MH bases smooth(); // Smooth the mesh with a given eigenfunctions return viewer.launch(); } |
Output:
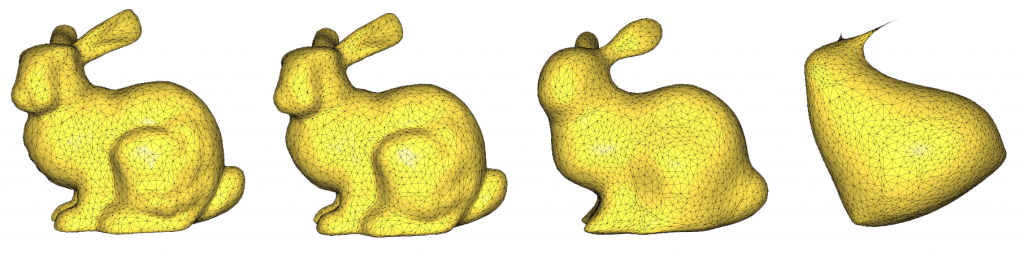
Ambient Occlusion Results:

